Why Julia ?

I gave a talk a couple weeks ago at the Tucson Python MeetUp about how Julia and Python can
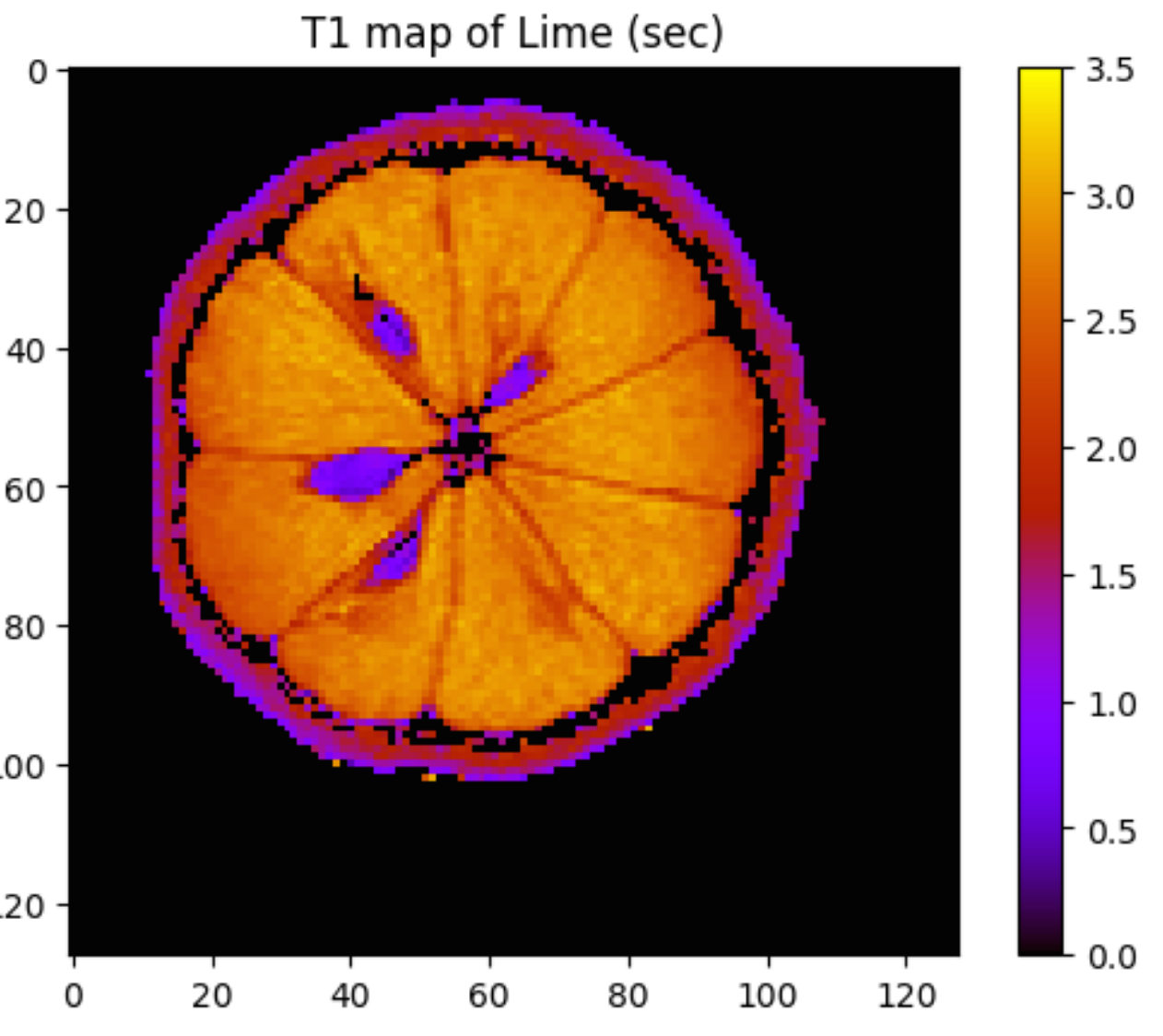
be used to analyze medical images. It turns out that for a simple processing task of calculating a T1 map of a lemon Julia is ~10X faster than Python and ~635X faster than Matlab. Besides speed, Julia offers great features:

1. General purpose programming language
2. Designed for scientific computing
3. Aims to solve the two language issue
4. Just-in-time compiling
5. Great Packaging system
6. Call C / C++ directly
7. Call Python directly
8. Metaprogramming
9. Multiple Dispatch

How to perform non-linear regression in Julia?

The objective of this analysis was to estimate the T1 time (seconds) for all pixels in the MRI of a lime. The assumed function is an exponential recovery of the form y = 1-exp(- x / T1). The Julia and Python notebooks are here.

# if you don't have LsqFit
Pkg.add("LsqFit")

# Load Packages
using LsqFit
using PyPlot

# "collect" some data
ydata = [0.09, 0.03,  0.23,  0.54,  0.67, 0.78,  0.80, 0.91,  1.07 ]
xdata = [0.0,.1,.5, 1., 1.5, 2, 3,5, 10]

# define function for exponential recovery
T1rec(x_, p) = p[1] * (1 - exp(-x_/p[2]) )

# fit data to the exponential recovery
initial_guess = [1., 2.]
fit = curve_fit(T1rec, xdata, ydata, initial_guess);
T1 = round(fit.param[2],3)
T1error = round( estimate_errors(fit, 0.95)[2], 3)
print("The estimated T1 is $T1, with an error of $T1error seconds")

# predict curve and plot it
plot(xdata,ydata,"o");
plot(xdata, T1rec(xdata, fit.param))
legend(["Observed","Fitted"])
xlabel("Time (sec)")
ylabel("Signal")

I applied a similar strategy to calculate the map below using Python and Julia_vs_Python. For details go here.